Sam Blackburn
Chewing Gum
Experiment
The aim of this experiment will be to investigate the physical properties of chewing gum: why it sticks to things and how its cohesive and adhesive properties can be affected.
Summary (written retrospectively):
The question “what do you do if you get chewing gum stuck in your hair?” posed by a certain episode of “The Simpsons” is a difficult one to answer. Finding an answer involved studying cohesive and adhesive forces, finding out how they are affected by various other factors and trying to look for some way to make the cohesive forces great enough that the gum can simply be pulled away. This is easier said than done and the mathematical modeling involved gets quite complicated. Although a little troubled by spurious and inaccurate results, some interesting conclusions are drawn here about chewing gum and its similarities and differences to Blu-Tak, another cohesive/adhesive substance.
Correction.
Contrary to the pretty graphics on Page Two (from www.wrigley.com) I will only be using Spearmint chewing gum for the investigation. Here is a revised version of the graphics that takes this important fact into account:
This is also the first
time I have been allowed to chew gum in a lesson… let alone charge it to
the school! Clearly my next practical
will have to be on champagne. Perhaps on the effect of careful pouring upon
preservation of effervescence.
Day One.
Attempts to dissolve chewing gum proved futile in both polar and non-polar solvents (water and methylated spirits). It would not even soften. The water dissolved the sugar from its surface, and if the water was mostly dried off, the gum became quite adhesive.
A tiny piece (about 0.5mm long) of chewing gum was placed on a microscope slide with a blob of water. It was examined, drawn and compared with another piece that had been chewed for 5 minutes. The observations are on a handwritten sheet.
Actually, this was far from perfect. I could have improved the image by staining the gum with an indicator, maybe iodine, as I was taught years ago in Biology. I’m not sure if this would have worked – chewing gum probably doesn’t contain starch.
The conclusion is that (this is the image and drawing it much larger.) and the
gum appears to be made of round blobs. It is at this point that the 3D nature
of the universe becomes annoying as the whole of the final picture was never in
focus at the same time.
Chewed gum is very
different. All the larger features are gone and the edge appears absolutely
smooth until you zoom in a very long way. It is here that I can compare with an
experiment I did before: Blu-Tak under a microscope consists of separate
fibres, and goo that holds the fibres together, creating a material with
interesting properties. Chewing gum has no visible fibres and clear from looking at the pictures…) unchewed gum appears to have a
fractal shape: every time you zoom in, more detail emerges, and the details at high factors of magnification look
much like those at the lower factors. This is true until we reach about
80,000:1 (No, the school microscopes won’t go that high. I was just looking at
one small piece of looks, under a microscope, as if it is made from a
homogeneous mixture of substances. This should give it different propertied to
the Blu-Tak.
Finally, the
ingredients list revealed nothing. “Gum base” is obviously what I am looking
for, but no clue was given as to its constituents or origin. I’m not even sure
if it’s vegetarian.
Day Two.
First of all, verified that iodine does not
stain gum. This means that gum contains no starch and also that I cannot think
of a way to improve the pictures I drew yesterday. Chewed gum showed no change
either, except that a few dislodged bits of cheek tissue turned black. Nice.
I needed to test
some physical properties. Tensile strength inside gum will be hard to measure
as it will be hard to roll a piece of gum into a cylinder of known and constant
diameter and then stretch that cylinder, without it sticking to everything it
touches.
One property of
Blu-Tak that I noticed before was that its adhesive forces are stronger than
its cohesive forces at low speeds, while the opposite is true at high speeds.
This means that however well a piece of Blu-Tak is stuck to something, it can
be cleanly removed if pulled away fast enough. The same is clearly not true
with chewing gum. The presence of fibres in Blu-Tak could probably be used to
explain this somehow.
I first attempted to
test the tensile forces of an unchewed piece of gum. It needed a thinnest point
at which it would snap, so I punched holes in it using… guess what… a common
stationery hole punch. I used 10g masses as clamps to grip the ends of the
stick and then fed string through the holes in the masses to exert a force. The
idea was that I would know the cross-sectional area of the stick as I could
easily measure the width (20mm), subtract twice the diameter of a hole (5mm)
and multiply that by its thickness (1.25mm).
Needless to say, it failed. The string cut into the chewing gum and it
broke at one end, despite the larger overall stress being halfway along.
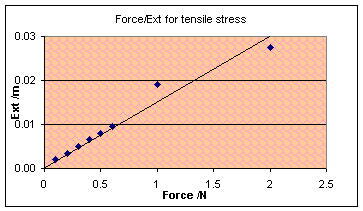
The graph shows a
more or less linear relationship between force and extension, until it
approaches breaking stress when the wrong bit broke anyway.
I tried another
experiment purely to test the adhesive forces of unchewed gum. A stick of gum
was washed to remove the sugar coating. It was then placed between two sheets
of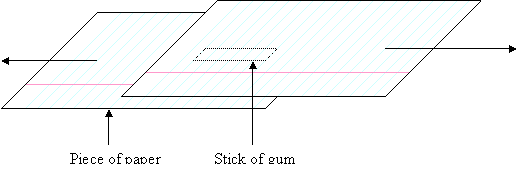 
paper and a compression force of 2N was applied
by placing masses on top.
Using string, a pulley and masses, forces were
then applied to the pieces of paper, (the arrows) and the paper slid over the
gum. The paper seemed too wet to stick to the gum, so I tried again, using the
same stick and new sheets of paper. It was drier the second time because some
water had been soaked up by the paper the first time.
By the fourth time,
the gum was actually sticking to the paper. This was not pleasant so I threw it
away. The graphs of these experiments show, again, a linear force/extension
graph.
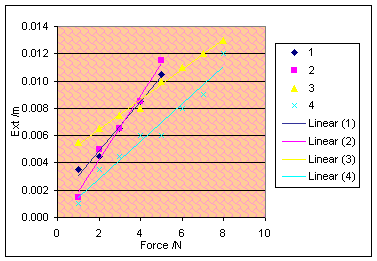
However, this graph
line changes in odd ways, as the gum gets drier. The overall, but not very
strong trend is that the adhesive forces become stronger when the gum is drier,
but I would not call this at all conclusive.
I did also try using
chewed gum between the sheets instead of unchewed gum. This worked but no
quantitative results were taken, as this experiment was not very scientifically
carried out. One observation I did make was that the adhesive forces were no
longer being tested. With chewed gum, the blob of gum split in half leaving
some stuck to each sheet, so the cohesive forces were the weaker forces.
Clearly, what was going on in chewed gum needed further investigation.
Day Three.
I plan to carry on
with the experiment I worked out yesterday: two sheets of paper, some chewed
gum in between and some forces. First, I will sort out what variables I can
change:
|
·
Horizontal
Force |
- The force
applied to try and shear/stretch the gum. |
|
·
Time
stretched |
- Sounds like a
term to describe the Tardis. |
|
·
Time
chewed |
- Like a paper
jam in a time machine. |
|
·
Temperature |
- Well, it
affects just about everything. |
|
·
Vertical
Force |
- The weight of
the mass placed on top. |
There are probably
others too (surface of paper…). I think I will start by varying the horizontal
force. To speed up measurement taking, I will not write down every value. I
will instead place a mark on the string and a sheet of paper under it, drawing
the position of the mark on the paper at the required times and measuring afterwards.
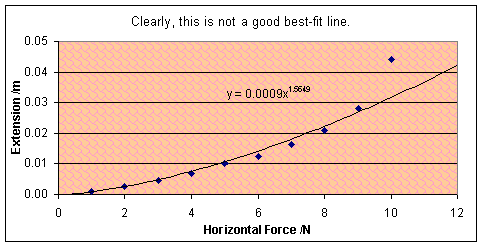There were lots of numerical results today. By
gradually loading up the above experiment and taking extension readings, I
built up a picture of the force/extension graph for chewing gum. The biggest
surprise is that it’s not linear. Not even remotely. If you don’t believe it,
look at the graph. The curve does not fit an exponential (ex) best
fit, or a power (y=xa, drawn onto graph) line either.
This turned out to
be no error: this graph results every time. The curve should be named after me.
Chewing gum behaves
very differently when its cohesive forces are being tested – i.e. in odd ways
as the graph above suggests – to when its adhesive forces are being tested,
when a nice linear graph results.
It would seem that
some long, boring maths is necessary here. I’ll have a go at it tomorrow.
Day Four.
x 0.02m R
It’s mathematics time.
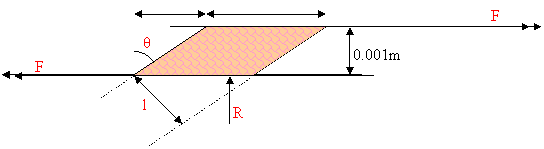
I approximate the
cross section of the piece of chewing gum to a parallelogram. I do this because
it makes life easy. Using a ruler I measured the length and width of a piece of
gum to be about 20mm, and using a micrometer I measured the thickness to be
about 1mm. These measurements were not very accurate as each bit of gum came
out a slightly different shape! This was probably the cause of my very
inconsistent results. The horizontal force F is
trying to shear the gum, which was initially rectangular, to this parallelogram
shape. The stress in the gum due to F can be
calculated:
Where w is the width
of the gum. But l has not been measured: this
formula will only be useful in terms of x. From
the diagram:
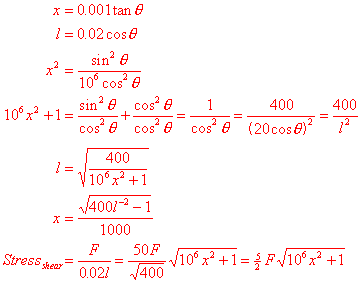
Which gives us the
shear stress in terms of the force and extension. I’m not quite sure what I’m
looking for here, but the compressive stress from the vertical force R is probably also involved:
Everything until now
is definitely true, although some approximations have been made. What I will do
now is make a conjecture, which I intend to test to see if it could be true.
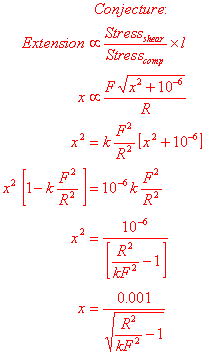
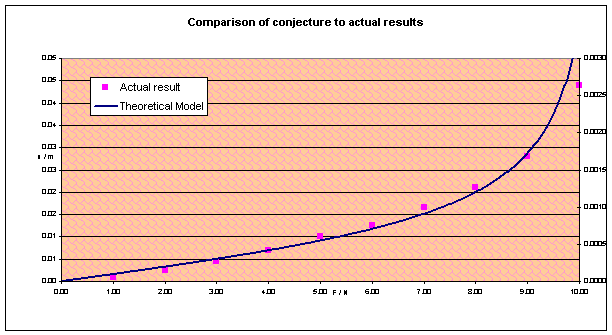Plotting x
against F gives this graph:
Which, with some fiddling of the constant k, gives a surprisingly good fit. The only big problem with the model is noticed when you see that the theoretical model actually uses the right hand y-axis, and requires a completely different scale! (The experimental result was chewed for 180s, temperature 298K, 2N vertical force.)
Now for some
practical work: today I plan to measure the effect upon shear strength (i.e.
the above experiment) of chewing the gum for longer or shorter periods before
shearing it. This is a hard one to predict. While gum is being chewed, two
things are going on: the teeth are constantly deforming the gum, and this tends
to affect most materials over time. There are also enzymes in saliva that are
trying to break down the gum and these may be able to soften it a little.
The experiment that I am now used to doing was repeated after chewing
for 60, 120, 180, 240, 300 seconds and once for 780 seconds after a… slight
timing error. The results are shown below, one graph with a horizontal force of
1N used and the other with a force of 2N. In both cases, the temperature was
298K, vertical force 2N.
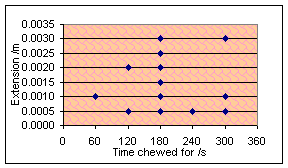
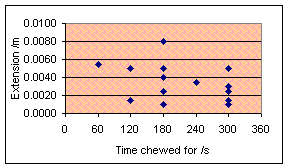
Oh well. As far as I can tell, there is absolutely no correlation there
whatsoever. However, if you can join the dots right you might be able to draw a
shipwreck.
Day Five.
Today I plan to change a variable that will actually make a difference.
I had noticed that if the horizontal force were applied to the experiment for a
long time, the extension would gradually increase. However, I am not sure that
this increase will be linear. In fact, I think that it is quite unlikely that
the speed will be constant.
When I studied Blu-Tak, I measured its reaction to tensile stress and
predicted an inverse curve: the extension would gradually increase and then
peak at a vertical asymptote. The experimental result looked approximately like
this but showed a definite linear region before it started to curve upwards.
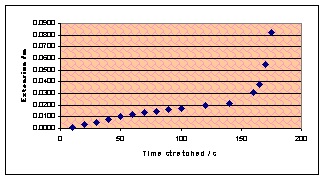Back to chewing gum, a force was applied to the
experiment and a reading was taken every few seconds, the time interval
depending upon roughly how fast it was moving (when it looked more or less
stationary, this was about a minute; when it was moving it tended to be about
five seconds).
As the graph shows, the relationship is not at all linear. This is a
very strange graph as the speed actually decreases near the beginning. I think
it’s mathematics time again, to try and model just what is going on.
Time to brush up on a few differential equations… It seems sensible that
the creep (rate of change of ext with respect to time) should be proportional
to the stress due to shear forces divided by the stress due to compressive
forces, and multiplied by the length of the distance being stretched.
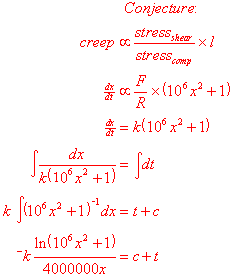
Since I can’t make x the subject of the above formula, I used my computer to plot it on a graph. I’ve plotted one of the experimental results too.
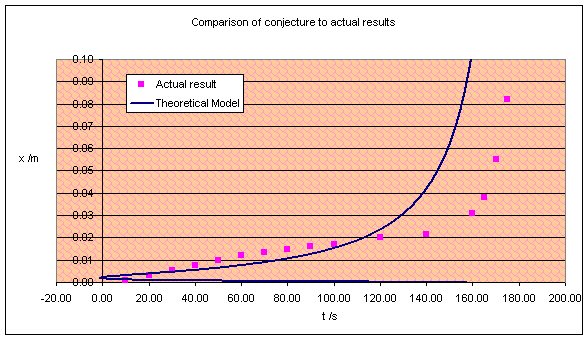
Oh dear. The model shows no resemblance whatsoever to the experiment!
Clearly the conjecture was a little wrong. The problem here is that the speed
actually decreases before the failure, which the model was unable to verify.
The gum must become stronger with time, creeping less and less, until a certain
point when it begins to fail and the line curves upwards (the model agrees on
this part at least).
This surprises me. In the Blu-Tak experiment I concluded that the fibres
in Blu-Tak could be aligned by a tensile force, thus increasing its strength.
However, gum has no fibres (according to the microscope observations) and
should not do this – but it does!
One other result today – by doing the experiment without gum, the coeff.
Of friction between two sheets of paper is 0.3.
Day Six.
Time for another variable, I feel, and temperature sounds like an
interesting one to do. Blu-Tak was greatly affected by temperature – it
softened when hot and became stronger (but not brittle) when cooled. Chewing
gum should do roughly the same thing, I think, although quantitative formulae
may be very different. I will carry out the usual experiment but at a range of
temperatures from 10ºC (the lowest I can easily expect to reach using the
school’s supply of not-very-frozen ice) and 50ºC (ditto with not-very-hot
boiling water).
During the experiment I noticed a difference in the appearance of hot
gum after it had been sheared. Yuk, was my thought. I was, unsurprisingly,
unable to quantify this in any useful way. Quantitative results were not
excellent today – The graphs all show a slight positive tendency but the
correlation is terrible. The ones for horizontal forces of 1N and 8N look the
most convincing:
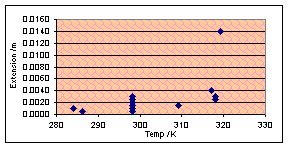
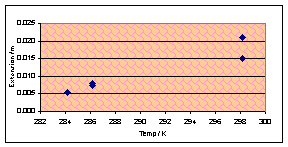
(Vertical force 2N, chewed 180s)
However there is insufficient evidence to justify or reject that the
relationship may be linear – or the same as with Blu-Tak.
Day Seven.
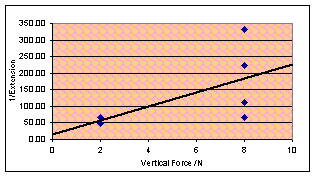Last day today – I need a finale. The vertical
force is the only thing left to change – and I feel fairly confident that
increasing the vertical force will make the gum stronger, thus reducing the
extension. An inverse relationship between vertical force and extension seems
quite likely to me, and this is what both my models predicted, although one of
them turned out to be wrong.
Sadly, due to time restrictions (school policy is just under 11 hours
maximum time for practical) I only got in one value other than the 2N I had
been using until now. The value was 8N and the (not very numerous) results are
plotted on this empty looking graph. Due to Excel not being able to plot an
inverse best fit, I have made the y-axis 1/Extension to look for
proportionality. The result is definitely correlated in the right direction,
but rather scattered and with too few values to justify proportionality.
Conclusion.
There are many conclusions to be made to this experiment, and many more
unanswered questions. I am very pleased that one of my theoretical models
fitted so well, but I am puzzled at the results that I failed to accurately
model.
Anomalous results were a large problem for this investigation. The first
cause of these could have been conditions in my mouth, but I think adequate
care was taken here: I drank 100ml of tap water 30s before chewing each stick
of gum to try and ensure that I was not dehydrated. The most likely cause, I
would say, is that the 1mm thickness and 20mm width of a blob of gum squished
between two sheets of paper were not always that size. If the gum was slightly
flatter, it would clearly have shown greater apparent strength, and I think
that this was the cause of the very bad results of the last few days. This idea
is backed up by the fact that results that were all taken from one experiment,
i.e. the ones taken on the first few days using the same gum and adding masses,
were very well correlated and consistent.
However, the one important conclusion is that you cannot get chewing gum
out of your hair. Even when heated or cooled, chewing gum is more adhesive than
cohesive, although the difference is lessened when it is cooled, and so an
attempt to pull it away will always leave most of it behind in a sticky mess.
The physicists have failed to remove chewing gum, and any further investigation
should be done in the chemistry department.
Appendix
On the next few pages is a long, boring table. To find what you are
looking for, I recommend loading the spreadsheet version instead, to which I
have added a brilliant little facility that compares any variables you choose,
and it also includes the working behind all the above graphs.
ALL RESULTS |
|
|
|
|
|
|
|
Time
chewed for /s |
Temperature
/K |
Vertical
Force /N |
Horizontal
force /N |
Time stretched /s |
Extension
/m |
Day |
|
|
|
|
|
|
|
|
|
60 |
298 |
2 |
1 |
0 |
0.0010 |
3 |
|
60 |
298 |
2 |
2 |
0 |
0.0055 |
3 |
|
60 |
298 |
2 |
3 |
0 |
0.0095 |
3 |
|
180 |
298 |
2 |
1 |
0 |
0.0030 |
3 |
|
180 |
298 |
2 |
2 |
0 |
0.0050 |
3 |
|
180 |
298 |
2 |
1 |
0 |
0.0020 |
3 |
|
180 |
298 |
2 |
2 |
0 |
0.0040 |
3 |
|
180 |
298 |
2 |
3 |
0 |
0.0060 |
3 |
|
180 |
298 |
2 |
4 |
0 |
0.0080 |
3 |
|
180 |
298 |
2 |
1 |
0 |
0.0015 |
3 |
|
180 |
298 |
2 |
2 |
0 |
0.0025 |
3 |
|
180 |
298 |
2 |
3 |
0 |
0.0045 |
3 |
|
300 |
298 |
2 |
1 |
0 |
0.0030 |
3 |
|
300 |
298 |
2 |
2 |
0 |
0.0050 |
3 |
|
300 |
298 |
2 |
3 |
0 |
0.0065 |
3 |
|
300 |
298 |
2 |
4 |
0 |
0.0080 |
3 |
|
300 |
298 |
2 |
5 |
0 |
0.0100 |
3 |
|
60 |
298 |
2 |
3 |
15 |
0.0030 |
3 |
|
60 |
298 |
2 |
3 |
30 |
0.0060 |
3 |
|
60 |
298 |
2 |
3 |
45 |
0.0080 |
3 |
|
60 |
298 |
2 |
3 |
60 |
0.0110 |
3 |
|
60 |
298 |
2 |
3 |
120 |
0.0190 |
3 |
|
60 |
298 |
2 |
3 |
180 |
0.0250 |
3 |
|
60 |
298 |
2 |
3 |
240 |
0.0310 |
3 |
|
60 |
298 |
2 |
3 |
300 |
0.0370 |
3 |
|
60 |
298 |
2 |
3 |
360 |
0.0440 |
3 |
|
60 |
298 |
2 |
3 |
410 |
0.0580 |
3 |
|
60 |
298 |
2 |
3 |
420 |
0.0650 |
3 |
|
60 |
298 |
2 |
3 |
425 |
0.0750 |
3 |
|
180 |
298 |
2 |
2 |
30 |
0.0010 |
3 |
|
180 |
298 |
2 |
2 |
60 |
0.0020 |
3 |
|
180 |
298 |
2 |
2 |
360 |
0.0045 |
3 |
|
180 |
298 |
2 |
2 |
480 |
0.0065 |
3 |
|
180 |
298 |
2 |
2 |
660 |
0.0085 |
3 |
|
180 |
298 |
2 |
2 |
1320 |
0.0100 |
3 |
|
180 |
298 |
2 |
4 |
10 |
0.0025 |
3 |
|
180 |
298 |
2 |
4 |
20 |
0.0065 |
3 |
|
180 |
298 |
2 |
4 |
30 |
0.0100 |
3 |
|
180 |
298 |
2 |
4 |
40 |
0.0130 |
3 |
|
180 |
298 |
2 |
4 |
50 |
0.0160 |
3 |
|
180 |
298 |
2 |
4 |
60 |
0.0180 |
3 |
|
180 |
298 |
2 |
4 |
70 |
0.0215 |
3 |
|
180 |
298 |
2 |
4 |
80 |
0.0250 |
3 |
|
180 |
298 |
2 |
4 |
90 |
0.0320 |
3 |
|
180 |
298 |
2 |
4 |
100 |
0.0420 |
3 |
|
180 |
298 |
2 |
4 |
110 |
0.0660 |
3 |
|
180 |
298 |
2 |
3 |
20 |
0.0060 |
3 |
|
180 |
298 |
2 |
3 |
40 |
0.0110 |
3 |
|
180 |
298 |
2 |
3 |
60 |
0.0150 |
3 |
|
180 |
298 |
2 |
3 |
80 |
0.0180 |
3 |
|
180 |
298 |
2 |
3 |
180 |
0.2150 |
3 |
|
180 |
298 |
2 |
3 |
280 |
0.2550 |
3 |
|
180 |
298 |
2 |
5 |
10 |
0.0015 |
3 |
|
180 |
298 |
2 |
5 |
20 |
0.0040 |
3 |
|
180 |
298 |
2 |
5 |
30 |
0.0055 |
3 |
|
180 |
298 |
2 |
5 |
40 |
0.0085 |
3 |
|
180 |
298 |
2 |
5 |
50 |
0.0100 |
3 |
|
180 |
298 |
2 |
5 |
60 |
0.0120 |
3 |
|
180 |
298 |
2 |
5 |
70 |
0.0145 |
3 |
|
180 |
298 |
2 |
5 |
80 |
0.0170 |
3 |
|
180 |
298 |
2 |
5 |
90 |
0.0190 |
3 |
|
180 |
298 |
2 |
5 |
100 |
0.0210 |
3 |
|
180 |
298 |
2 |
5 |
110 |
0.0235 |
3 |
|
180 |
298 |
2 |
5 |
120 |
0.0300 |
3 |
|
180 |
298 |
2 |
5 |
130 |
0.0370 |
3 |
|
180 |
298 |
2 |
5 |
135 |
0.0440 |
3 |
|
180 |
298 |
2 |
5 |
140 |
0.0490 |
3 |
|
180 |
298 |
2 |
5 |
145 |
0.0550 |
3 |
|
180 |
298 |
2 |
5 |
150 |
0.0670 |
3 |
|
120 |
298 |
2 |
1 |
0 |
0.0020 |
4 |
|
120 |
298 |
2 |
2 |
0 |
0.0050 |
4 |
|
120 |
298 |
2 |
3 |
0 |
0.0090 |
4 |
|
120 |
298 |
2 |
1 |
0 |
0.0005 |
4 |
|
120 |
298 |
2 |
2 |
0 |
0.0015 |
4 |
|
120 |
298 |
2 |
3 |
0 |
0.0030 |
4 |
|
120 |
298 |
2 |
4 |
0 |
0.0050 |
4 |
|
120 |
298 |
2 |
5 |
0 |
0.0095 |
4 |
|
180 |
298 |
2 |
1 |
0 |
0.0025 |
4 |
|
180 |
298 |
2 |
2 |
0 |
0.0080 |
4 |
|
180 |
298 |
2 |
3 |
0 |
0.0110 |
4 |
|
240 |
298 |
2 |
1 |
0 |
0.0005 |
4 |
|
240 |
298 |
2 |
2 |
0 |
0.0035 |
4 |
|
240 |
298 |
2 |
3 |
0 |
0.0045 |
4 |
|
300 |
298 |
2 |
1 |
0 |
0.0005 |
4 |
|
300 |
298 |
2 |
2 |
0 |
0.0025 |
4 |
|
300 |
298 |
2 |
3 |
0 |
0.0040 |
4 |
|
300 |
298 |
2 |
4 |
0 |
0.0060 |
4 |
|
780 |
298 |
2 |
1 |
0 |
0.0010 |
4 |
|
780 |
298 |
2 |
2 |
0 |
0.0025 |
4 |
|
780 |
298 |
2 |
3 |
0 |
0.0050 |
4 |
|
120 |
298 |
2 |
3 |
20 |
0.0035 |
4 |
|
120 |
298 |
2 |
3 |
40 |
0.0070 |
4 |
|
120 |
298 |
2 |
3 |
60 |
0.0115 |
4 |
|
120 |
298 |
2 |
3 |
80 |
0.0160 |
4 |
|
120 |
298 |
2 |
3 |
100 |
0.0170 |
4 |
|
120 |
298 |
2 |
3 |
120 |
0.0185 |
4 |
|
120 |
298 |
2 |
3 |
140 |
0.0205 |
4 |
|
120 |
298 |
2 |
3 |
160 |
0.0230 |
4 |
|
120 |
298 |
2 |
3 |
180 |
0.0255 |
4 |
|
120 |
298 |
2 |
3 |
200 |
0.0285 |
4 |
|
120 |
298 |
2 |
3 |
220 |
0.0300 |
4 |
|
120 |
298 |
2 |
3 |
240 |
0.0345 |
4 |
|
120 |
298 |
2 |
3 |
260 |
0.0365 |
4 |
|
120 |
298 |
2 |
3 |
280 |
0.0385 |
4 |
|
120 |
298 |
2 |
3 |
300 |
0.0435 |
4 |
|
120 |
298 |
2 |
3 |
310 |
0.0620 |
4 |
|
120 |
298 |
2 |
3 |
320 |
0.1090 |
4 |
|
120 |
298 |
2 |
5 |
5 |
0.0015 |
4 |
|
120 |
298 |
2 |
5 |
10 |
0.0025 |
4 |
|
120 |
298 |
2 |
5 |
15 |
0.0045 |
4 |
|
120 |
298 |
2 |
5 |
20 |
0.0060 |
4 |
|
120 |
298 |
2 |
5 |
25 |
0.0080 |
4 |
|
120 |
298 |
2 |
5 |
30 |
0.0105 |
4 |
|
120 |
298 |
2 |
5 |
35 |
0.0125 |
4 |
|
120 |
298 |
2 |
5 |
40 |
0.0145 |
4 |
|
120 |
298 |
2 |
5 |
45 |
0.0160 |
4 |
|
120 |
298 |
2 |
5 |
50 |
0.0170 |
4 |
|
120 |
298 |
2 |
5 |
55 |
0.0180 |
4 |
|
120 |
298 |
2 |
5 |
60 |
0.0190 |
4 |
|
120 |
298 |
2 |
5 |
90 |
0.0240 |
4 |
|
120 |
298 |
2 |
5 |
120 |
0.0260 |
4 |
|
120 |
298 |
2 |
5 |
150 |
0.0340 |
4 |
|
120 |
298 |
2 |
5 |
153 |
0.0810 |
4 |
|
240 |
298 |
2 |
3 |
10 |
0.0015 |
4 |
|
240 |
298 |
2 |
3 |
15 |
0.0020 |
4 |
|
240 |
298 |
2 |
3 |
25 |
0.0035 |
4 |
|
240 |
298 |
2 |
3 |
35 |
0.0055 |
4 |
|
240 |
298 |
2 |
3 |
40 |
0.0065 |
4 |
|
240 |
298 |
2 |
3 |
50 |
0.0070 |
4 |
|
240 |
298 |
2 |
3 |
60 |
0.0100 |
4 |
|
240 |
298 |
2 |
3 |
70 |
0.0110 |
4 |
|
240 |
298 |
2 |
3 |
90 |
0.0120 |
4 |
|
240 |
298 |
2 |
3 |
120 |
0.0150 |
4 |
|
240 |
298 |
2 |
3 |
150 |
0.0165 |
4 |
|
240 |
298 |
2 |
3 |
240 |
0.0210 |
4 |
|
240 |
298 |
2 |
3 |
480 |
0.0265 |
4 |
|
240 |
298 |
2 |
3 |
660 |
0.0330 |
4 |
|
300 |
298 |
2 |
4 |
10 |
0.0010 |
4 |
|
300 |
298 |
2 |
4 |
20 |
0.0030 |
4 |
|
300 |
298 |
2 |
4 |
30 |
0.0055 |
4 |
|
300 |
298 |
2 |
4 |
40 |
0.0075 |
4 |
|
300 |
298 |
2 |
4 |
50 |
0.0100 |
4 |
|
300 |
298 |
2 |
4 |
60 |
0.0120 |
4 |
|
300 |
298 |
2 |
4 |
70 |
0.0135 |
4 |
|
300 |
298 |
2 |
4 |
80 |
0.0150 |
4 |
|
300 |
298 |
2 |
4 |
90 |
0.0160 |
4 |
|
300 |
298 |
2 |
4 |
100 |
0.0170 |
4 |
|
300 |
298 |
2 |
4 |
120 |
0.0200 |
4 |
|
300 |
298 |
2 |
4 |
140 |
0.0215 |
4 |
|
300 |
298 |
2 |
4 |
160 |
0.0310 |
4 |
|
300 |
298 |
2 |
4 |
165 |
0.0380 |
4 |
|
300 |
298 |
2 |
4 |
170 |
0.0550 |
4 |
|
300 |
298 |
2 |
4 |
175 |
0.0820 |
4 |
|
780 |
298 |
2 |
3 |
5 |
0.0020 |
4 |
|
780 |
298 |
2 |
3 |
10 |
0.0035 |
4 |
|
780 |
298 |
2 |
3 |
15 |
0.0050 |
4 |
|
780 |
298 |
2 |
3 |
20 |
0.0070 |
4 |
|
780 |
298 |
2 |
3 |
25 |
0.0095 |
4 |
|
780 |
298 |
2 |
3 |
30 |
0.0115 |
4 |
|
780 |
298 |
2 |
3 |
35 |
0.0125 |
4 |
|
780 |
298 |
2 |
3 |
40 |
0.0135 |
4 |
|
780 |
298 |
2 |
3 |
60 |
0.0170 |
4 |
|
780 |
298 |
2 |
3 |
80 |
0.0190 |
4 |
|
780 |
298 |
2 |
3 |
180 |
0.0225 |
4 |
|
780 |
298 |
2 |
3 |
240 |
0.0245 |
4 |
|
780 |
298 |
2 |
3 |
360 |
0.0320 |
4 |
|
780 |
298 |
2 |
3 |
480 |
0.0370 |
4 |
|
780 |
298 |
2 |
3 |
720 |
0.0550 |
4 |
|
780 |
298 |
2 |
3 |
730 |
0.0780 |
4 |
|
780 |
298 |
2 |
3 |
732 |
0.1430 |
4 |
|
180 |
298 |
2 |
1 |
0 |
0.0010 |
5 |
|
180 |
298 |
2 |
2 |
0 |
0.0025 |
5 |
|
180 |
298 |
2 |
3 |
0 |
0.0045 |
5 |
|
180 |
298 |
2 |
4 |
0 |
0.0070 |
5 |
|
180 |
298 |
2 |
5 |
0 |
0.0100 |
5 |
|
180 |
298 |
2 |
6 |
0 |
0.0125 |
5 |
|
180 |
298 |
2 |
7 |
0 |
0.0165 |
5 |
|
180 |
298 |
2 |
8 |
0 |
0.0210 |
5 |
|
180 |
298 |
2 |
9 |
0 |
0.0280 |
5 |
|
180 |
298 |
2 |
10 |
0 |
0.0440 |
5 |
|
180 |
298 |
2 |
1 |
0 |
0.0005 |
5 |
|
180 |
298 |
2 |
2 |
0 |
0.0010 |
5 |
|
180 |
298 |
2 |
3 |
0 |
0.0020 |
5 |
|
180 |
298 |
2 |
4 |
0 |
0.0025 |
5 |
|
180 |
298 |
2 |
5 |
0 |
0.0040 |
5 |
|
180 |
298 |
2 |
6 |
0 |
0.0070 |
5 |
|
180 |
298 |
2 |
7 |
0 |
0.0110 |
5 |
|
180 |
298 |
2 |
8 |
0 |
0.0150 |
5 |
|
300 |
298 |
2 |
1 |
0 |
0.0010 |
5 |
|
300 |
298 |
2 |
2 |
0 |
0.0030 |
5 |
|
300 |
298 |
2 |
3 |
0 |
0.0045 |
5 |
|
300 |
298 |
2 |
4 |
0 |
0.0065 |
5 |
|
300 |
298 |
2 |
5 |
0 |
0.0095 |
5 |
|
300 |
298 |
2 |
6 |
0 |
0.0140 |
5 |
|
300 |
298 |
2 |
7 |
0 |
0.0220 |
5 |
|
300 |
298 |
2 |
8 |
0 |
0.1050 |
5 |
|
300 |
298 |
2 |
1 |
0 |
0.0005 |
5 |
|
300 |
298 |
2 |
2 |
0 |
0.0010 |
5 |
|
300 |
298 |
2 |
3 |
0 |
0.0020 |
5 |
|
300 |
298 |
2 |
4 |
0 |
0.0025 |
5 |
|
300 |
298 |
2 |
5 |
0 |
0.0035 |
5 |
|
300 |
298 |
2 |
6 |
0 |
0.0050 |
5 |
|
300 |
298 |
2 |
7 |
0 |
0.0065 |
5 |
|
300 |
298 |
2 |
8 |
0 |
0.0086 |
5 |
|
300 |
298 |
2 |
9 |
0 |
0.0120 |
5 |
|
300 |
298 |
2 |
10 |
0 |
0.0170 |
5 |
|
300 |
298 |
2 |
11 |
0 |
0.0250 |
5 |
|
300 |
298 |
2 |
1 |
0 |
0.0005 |
5 |
|
300 |
298 |
2 |
2 |
0 |
0.0015 |
5 |
|
300 |
298 |
2 |
3 |
0 |
0.0025 |
5 |
|
300 |
298 |
2 |
4 |
0 |
0.0035 |
5 |
|
300 |
298 |
2 |
5 |
0 |
0.0055 |
5 |
|
300 |
298 |
2 |
6 |
0 |
0.0075 |
5 |
|
300 |
298 |
2 |
7 |
0 |
0.0110 |
5 |
|
300 |
298 |
2 |
8 |
0 |
0.0160 |
5 |
|
300 |
298 |
2 |
9 |
0 |
0.0290 |
5 |
|
180 |
319 |
2 |
1 |
0 |
0.0140 |
6 |
|
180 |
318 |
2 |
1 |
0 |
0.0030 |
6 |
|
180 |
318 |
2 |
1 |
0 |
0.0025 |
6 |
|
180 |
317 |
2 |
1 |
0 |
0.0040 |
6 |
|
180 |
309 |
2 |
1 |
0 |
0.0015 |
6 |
|
180 |
309 |
2 |
2 |
0 |
0.0040 |
6 |
|
180 |
309 |
2 |
3 |
0 |
0.0070 |
6 |
|
180 |
286 |
2 |
1 |
0 |
0.0005 |
6 |
|
180 |
286 |
2 |
2 |
0 |
0.0010 |
6 |
|
180 |
286 |
2 |
3 |
0 |
0.0015 |
6 |
|
180 |
286 |
2 |
4 |
0 |
0.0025 |
6 |
|
180 |
286 |
2 |
5 |
0 |
0.0040 |
6 |
|
180 |
286 |
2 |
6 |
0 |
0.0050 |
6 |
|
180 |
286 |
2 |
7 |
0 |
0.0060 |
6 |
|
180 |
286 |
2 |
8 |
0 |
0.0080 |
6 |
|
180 |
286 |
2 |
9 |
0 |
0.0100 |
6 |
|
180 |
286 |
2 |
10 |
0 |
0.0115 |
6 |
|
180 |
286 |
2 |
11 |
0 |
0.0145 |
6 |
|
180 |
286 |
2 |
12 |
0 |
0.0190 |
6 |
|
180 |
286 |
2 |
13 |
0 |
0.0250 |
6 |
|
180 |
286 |
2 |
1 |
0 |
0.0005 |
6 |
|
180 |
286 |
2 |
2 |
0 |
0.0010 |
6 |
|
180 |
286 |
2 |
3 |
0 |
0.0015 |
6 |
|
180 |
286 |
2 |
4 |
0 |
0.0025 |
6 |
|
180 |
286 |
2 |
5 |
0 |
0.0040 |
6 |
|
180 |
286 |
2 |
6 |
0 |
0.0050 |
6 |
|
180 |
286 |
2 |
7 |
0 |
0.0060 |
6 |
|
180 |
286 |
2 |
8 |
0 |
0.0075 |
6 |
|
180 |
286 |
2 |
9 |
0 |
0.0085 |
6 |
|
180 |
286 |
2 |
10 |
0 |
0.0095 |
6 |
|
180 |
286 |
2 |
11 |
0 |
0.0110 |
6 |
|
180 |
286 |
2 |
12 |
0 |
0.0125 |
6 |
|
180 |
284 |
2 |
1 |
0 |
0.0010 |
6 |
|
180 |
284 |
2 |
2 |
0 |
0.0025 |
6 |
|
180 |
284 |
2 |
3 |
0 |
0.0030 |
6 |
|
180 |
284 |
2 |
4 |
0 |
0.0035 |
6 |
|
180 |
284 |
2 |
5 |
0 |
0.0040 |
6 |
|
180 |
284 |
2 |
6 |
0 |
0.0045 |
6 |
|
180 |
284 |
2 |
7 |
0 |
0.0050 |
6 |
|
180 |
284 |
2 |
8 |
0 |
0.0055 |
6 |
|
180 |
284 |
2 |
9 |
0 |
0.0060 |
6 |
|
180 |
284 |
2 |
10 |
0 |
0.0070 |
6 |
|
180 |
284 |
2 |
11 |
0 |
0.0080 |
6 |
|
180 |
284 |
2 |
12 |
0 |
0.0100 |
6 |
|
180 |
284 |
2 |
13 |
0 |
0.0130 |
6 |
|
180 |
284 |
2 |
14 |
0 |
0.0200 |
6 |
|
180 |
284 |
2 |
15 |
0 |
0.0350 |
6 |
|
180 |
319 |
2 |
1 |
3 |
0.0070 |
6 |
|
180 |
319 |
2 |
1 |
6 |
0.0200 |
6 |
|
180 |
319 |
2 |
1 |
9 |
0.0410 |
6 |
|
180 |
318 |
2 |
1 |
5 |
0.0040 |
6 |
|
180 |
318 |
2 |
1 |
10 |
0.0080 |
6 |
|
180 |
318 |
2 |
1 |
15 |
0.0265 |
6 |
|
180 |
318 |
2 |
1 |
20 |
0.0490 |
6 |
|
180 |
318 |
2 |
1 |
5 |
0.0025 |
6 |
|
180 |
318 |
2 |
1 |
8 |
0.0070 |
6 |
|
180 |
318 |
2 |
1 |
11 |
0.0095 |
6 |
|
180 |
318 |
2 |
1 |
14 |
0.0125 |
6 |
|
180 |
318 |
2 |
1 |
17 |
0.0155 |
6 |
|
180 |
318 |
2 |
1 |
20 |
0.0200 |
6 |
|
180 |
318 |
2 |
1 |
23 |
0.0270 |
6 |
|
180 |
317 |
2 |
1 |
5 |
0.0020 |
6 |
|
180 |
317 |
2 |
1 |
10 |
0.0075 |
6 |
|
180 |
317 |
2 |
1 |
15 |
0.0190 |
6 |
|
180 |
317 |
2 |
1 |
20 |
0.0550 |
6 |
|
180 |
317 |
2 |
1 |
22 |
0.0890 |
6 |
|
180 |
309 |
2 |
3 |
5 |
0.0020 |
6 |
|
180 |
309 |
2 |
3 |
10 |
0.0040 |
6 |
|
180 |
309 |
2 |
3 |
15 |
0.0070 |
6 |
|
180 |
309 |
2 |
3 |
20 |
0.0100 |
6 |
|
180 |
309 |
2 |
3 |
25 |
0.0120 |
6 |
|
180 |
309 |
2 |
3 |
30 |
0.0140 |
6 |
|
180 |
309 |
2 |
3 |
35 |
0.0160 |
6 |
|
180 |
309 |
2 |
3 |
40 |
0.0180 |
6 |
|
180 |
309 |
2 |
3 |
45 |
0.0190 |
6 |
|
180 |
309 |
2 |
3 |
50 |
0.0210 |
6 |
|
180 |
309 |
2 |
3 |
55 |
0.0225 |
6 |
|
180 |
309 |
2 |
3 |
60 |
0.0235 |
6 |
|
180 |
309 |
2 |
3 |
90 |
0.0325 |
6 |
|
180 |
309 |
2 |
3 |
120 |
0.0410 |
6 |
|
180 |
309 |
2 |
3 |
150 |
0.0495 |
6 |
|
180 |
309 |
2 |
3 |
180 |
0.0595 |
6 |
|
180 |
309 |
2 |
3 |
210 |
0.0705 |
6 |
|
180 |
309 |
2 |
3 |
240 |
0.0830 |
6 |
|
180 |
309 |
2 |
3 |
245 |
0.0890 |
6 |
|
180 |
309 |
2 |
3 |
250 |
0.0940 |
6 |
|
180 |
309 |
2 |
3 |
255 |
0.0975 |
6 |
|
180 |
309 |
2 |
3 |
260 |
0.1050 |
6 |
|
180 |
284 |
8 |
15 |
2 |
0.0170 |
6 |
|
180 |
298 |
8 |
4 |
0 |
0.0010 |
7 |
|
180 |
298 |
8 |
8 |
0 |
0.0045 |
7 |
|
180 |
298 |
8 |
4 |
0 |
0.0040 |
7 |
|
180 |
298 |
8 |
8 |
0 |
0.0150 |
7 |
|
180 |
298 |
8 |
4 |
0 |
0.0040 |
7 |
|
180 |
298 |
8 |
8 |
0 |
0.0090 |
7 |
|
180 |
298 |
8 |
12 |
0 |
0.0290 |
7 |
|
180 |
298 |
8 |
4 |
0 |
0.0015 |
7 |
|
180 |
298 |
8 |
8 |
0 |
0.0030 |
7 |
|
180 |
298 |
8 |
12 |
0 |
0.0070 |
7 |
|
180 |
298 |
8 |
16 |
0 |
0.0140 |
7 |
|
300 |
298 |
8 |
4 |
0 |
0.0015 |
7 |
|
300 |
298 |
8 |
8 |
0 |
0.0045 |
7 |
|
300 |
298 |
8 |
12 |
0 |
0.0125 |
7 |
|
300 |
298 |
8 |
4 |
0 |
0.0010 |
7 |
|
300 |
298 |
8 |
8 |
0 |
0.0050 |
7 |
|
300 |
298 |
8 |
12 |
0 |
0.0012 |
7 |
|
300 |
298 |
8 |
16 |
0 |
0.0250 |
7 |
|
300 |
298 |
8 |
4 |
0 |
0.0030 |
7 |
|
300 |
298 |
8 |
8 |
0 |
0.0050 |
7 |
|
300 |
298 |
8 |
12 |
0 |
0.0140 |
7 |
|
300 |
298 |
8 |
16 |
0 |
0.0290 |
7 |
Appendix
On the last few pages is a long, boring table. To find what you are
looking for, I recommend loading the spreadsheet version instead, to which I
have added a brilliant little facility that compares any variables you choose,
and it also includes the working behind all the above graphs.